Miscellaneous Factors and FormulaeThis is a page of other conversion factors and formulae which might be useful when working on many projects, eg. temperature, currency (up-to-date), pressure - plus a few curiosities. Use these links to other pages of conversion factors. |
| Length | Area | Volume | Mass |
Currency Conversion
Click here to access a Currency Converter
Up-to-date exchange rates of 164 Worldwide currencies
Temperature Conversion
Degrees Fahrenheit °F to Degrees Centigrade C (Celsius °C)
C = (°F - 32) x 0.56
Degrees Centigrade C (Celsius °C) to Degrees Fahrenheit °F
°F = (C x 1.8) + 32
These two factors can be more easily remembered as five ninths (0.56) and nine fifths (1.8) respectively.
Try here to find out about our local weather.
When working with heating systems the output of a boiler can be given in Kilowatts (KW) or British Thermal Units (BTU), the conversion rate is 1KW = 3,412BTUs
There are four different ways that oven temperatures may be given in recipe books or marked on the controls.
| Fahrenheit °F | Gas Mark | Centigrade C | |
| Very Slow | 240 - 280 | ¼ - ½ | 115 - 135 |
| Slow | 280 - 320 | 1 | 135 - 160 |
| Warm | 320 - 340 | 3 | 160 - 170 |
| Moderate | 340 - 370 | 4 | 170 - 185 |
| Fairly Hot | 370 - 400 | 5 - 6 | 185 - 205 |
| Hot | 400 - 440 | 7 | 205 - 225 |
| Very Hot | 440 - 480 | 8 - 9 | 225 - 250 |
Pressure
| from | to | multiply by |
| Pounds-force per sq. inch (psi,lb/inch2) | Kilograms-force per square centimetre (kg/ cm2) | 0.070307 |
| Kilograms-force per square centimetre (kg/ cm2) | Pounds-force per sq. inch (psi,lb/inch2) | 14.2233 |
| Pounds-force per sq. inch (psi,lb/inch2) | Atmospheres (atm) | 0.068 |
| Atmospheres (atm) | Pounds-force per sq. inch (psi,lb/inch2) | 14.696 |
| Pounds-force per sq. inch (psi,lb/inch2) | Bars | 0.069 |
| Bars | Pounds-force per sq. inch (psi,lb/inch2) | 14.5038 |
| Pounds-force per sq. inch (psi,lb/inch2) | Millibar (mbar) | 68.947 |
| Millibar (mbar) | Pounds-force per sq. inch (psi,lb/inch2) | 0.0145 |
| Millibar (mbar) | Millimetres of mercury (mmHg) | 0.75 |
| Millimetres of mercury (mmHg) | Millibar (mbar) | 1.333 |
| Millibar (mbar) | Inches of water (inH2O) | 0.535 |
| Inches of water (inH2O) | Millibar (mbar) | 1.868 |
| Inches of water (inH2O) | Pounds-force per sq. inch (psi,lb/inch2) | 0.036 |
| Pounds-force per sq. inch (psi,lb/inch2) | Inches of water (inH2O) | 27.68 |
Speed
1 mph = 1.60934 km/h
1 km/h =0.621371 mph
Fuel Consumption
10 mpg = 28.25 litres/100 km
50 mpg = 5.65 litres/100 km
Power
An early definition of one Horsepower was the raising of 33,000 pounds at a rate of 1 foot per minute. This was an arbitrary figure chosen by James Watt to promote his steam engines. He carried out research which determined that on average a horse could raise about 22,000 pounds at 1 foot per minute. So he added one third and produced an engine that could raise 33,000 pounds at this rate to impress his potential customers and said that it was equal to what one horse could do. Afterwards it was accepted that defining the power of an engine would use the 33,000 figure.
The definition of one horsepower (hp.) as a unit of work is:-
Useful Formulae
Symbols used
or Pi = 3.14216d = diameter
r = radius = ½ the diameter
h = height
Circumference of a circle = x the diameter(d).
Area of a circle = x the radius x the radius(r).
3.1416 x r2
Area of a triangle = ½ the height x length of base.
Surface area of cone = slant height x ½ circumference of base.
h x x d
2
Curved surface area of cylinder = circumference x height x d x h
Total surface area of a cylinder = 2 x area of base + area of curved surface.
2( x r2) + x d x h
Surface area of sphere = 4 x x radius squared.
4 x 3.1416 x r2
Volume of a sphere = 4 x x radius x radius x radius divided by 3
4 x 3.1416 x r3
3
Volume of a cone = 3.1416 x radius squared x height(h) divided by 3.
3.1416 x r2 x h
3
Volume of a pyramid = area of the base x height divided by 3.
To make a set square
Use the 3, 4, 5 principal (from the Pythagoras Theorem), as a triangle made to these proportions will always have a 90° angle between the two shorter sides, ie. make a triangle from strips of timber 60cm, 80cm and 100cm (or any multiple of 3,4 and 5). Cut the timber slightly longer, placing the fixing screw or nail in the centre at the exact measurement - trim off the protruding overlaps to leave flush corners.
Golden Ratio
The Golden Ratio is a number which has been known since ancient times and has great significance in art, architecture and many other fields of study. It has a number of other names - Golden Mean, Golden Number, Golden Proportion, Golden Rule, Golden Section, Devine Proportion. It is usually represented by the Greek letter phi or 
with the value 1.61803398874984..... which is an irrational number. This means that when it is calculated the number of digits after the decimal point are infinite and do not repeat.
The ratio is usually quoted as 1.618 : 1 and can be found throughout nature, eg. the spirals in shells. It is said to show why we find things asthetic or pleasing to the eye. For example if you compare the proportions of parts of the body they have the relationship 1.618 : 1. It is thought that Leorardo da Vinci used it to define the features of the Mona Lisa and this is why she has such a captivating face.
In geometry the Golden Rectangle has sides to this proportion and if a square of the shorter side is removed the remaining rectangle has the same proportions ad infinitum. When designing we often create shapes and toy with them until they 'look right'. If the proportions are measured they usually comply to the Golden Ratio. Is it a coincidence that even credit cards are made the this proportion?
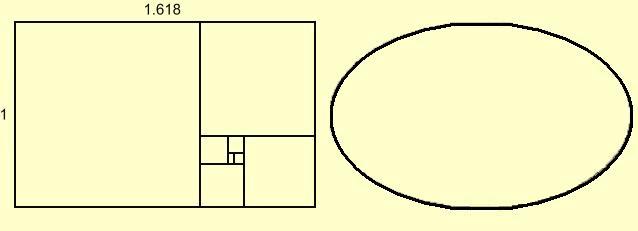
The rectangle and ellipse are drawn to the Golden Proportion.
The Pulse Rate at Different Ages
| Age | Beats per minute |
| Newly born | 130 to 140 |
| 1st year | 115 to 130 |
| 2nd year | 100 to 115 |
| 3rd year | 95 to 105 |
| 7 to 14 | 80 to 90 |
| 14 to 21 | 75 to 85 |
| 21 to 60 | 70 to 75 |
| over 60 | 75 to 85 |
To determine someones age. - something of a performance trick. Get the other person to work out the calculations and give the result.
| Start with month of birth eg. August | 8 | ||
| Multiply by 2 | 16 | ||
| Add 5 | 21 | ||
| Multiply by 50 | 1050 | ||
| Add their age eg. 20 | 1070 | ||
| Subtract 365 | 705 | ||
| Add 115 | 820 |
